PGStudy-统计学指标Part

发表于 2024-10-13 分类于专题， PGStudy 阅读次数： Waline：本文字数： 1.4k 阅读时长 ≈ 5 分钟

统计学指标——分类

基本概念

准确度、精确率、召回率、F1值作为评估指标，经常用到分类效果的评测上。比较好理解的二分类问题，准确度评估预测正确的比例，精确率评估预测正例的查准率，召回率评估真实正例的查全率。

准确度 Accuracy

准确度：正例和负例中预测正确数量占总数量的比例，用公式表示： \[ ACC=\frac{TP+TN}{TP+FP+FN+TN} \]

精确度 Precision

精确度：以预测结果为判断依据，预测为正例的样本中预测正确的比例。 \[ precision=\frac{TP}{TP+FP} \] 精确度还有一个名字，叫做“查准率”，我们关心的主要部分是正例，所以查准率就是相对正例的预测结果而言，正例预测的准确度。直白的意思就是模型预测为正例的样本中，其中真正的正例占预测为正例样本的比例，用此标准来评估预测正例的准确度。

召回率 Recall

召回率：以实际样本为判断依据，实际为正例的样本中，被预测正确的正例占总实际正例样本的比例。 \[ recall=\frac{TP}{TP+FN} \]

F1值

Q: 为什么在有了前三种评估预测的值后还需要F1值
A: 单独用精确率或者召回率是否能很好的评估模型好坏，举个例子：

1、什么情况下精确率很高但是召回率很低？

一个极端的例子，比如我们黑球实际上有3个，分别是1号、2号、3号球，如果我们只预测1号球是黑色，此时预测为正例的样本都是正确的，精确率p=1，但是召回率r=1/3。

2、什么情况下召回率很高但是精确率很低？

如果我们10个球都预测为黑球，此时所有实际为黑球都被预测正确了，实际上黑球有三个，召回率r=1，精确率p=3/10。

F1值就是中和了精确率和召回率的指标： \[ F1=\frac{2PR}{P+R} \] 当P和R同时为1时，F1=1。当有一个很大，另一个很小的时候，比如P=1，R_0，此时F10。分子2PR的2完全了为了使最终取值在0-1之间，进行区间放大，无实际意义。

多分类下的评估

Multiple-classification实际上是更广泛的二分类，即，二分类实际上是多分类的一种特殊情况，因为任何一种分类结果实际上都可以被当做Positives正例。即多分类在计算统计学指标时需要指定正例是谁。

值得注意的是对整体的评估指标应该如何求值，因为我们有多个正例的acc,p,r，一般情况下，直接求均值即可，但在有些时候，根据不同类重要性不同对其进行加权均值也是一种常见方式。

补充相关

什么是TP，FP，FN，TN

这四种分别是真正例(True Positives)，假正例(False Positives)，假负例(False Negatives)，真负例(True Negatives)

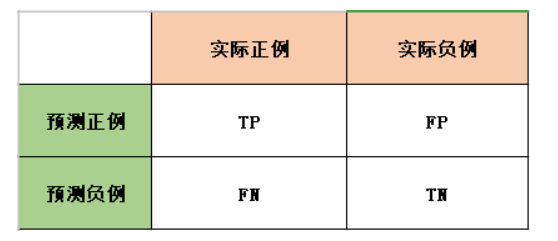
记忆要点：正负例的是依据预测值，真假是依据实际值。真正例的意思，预测为正例，实际上是真的正例。

eg：

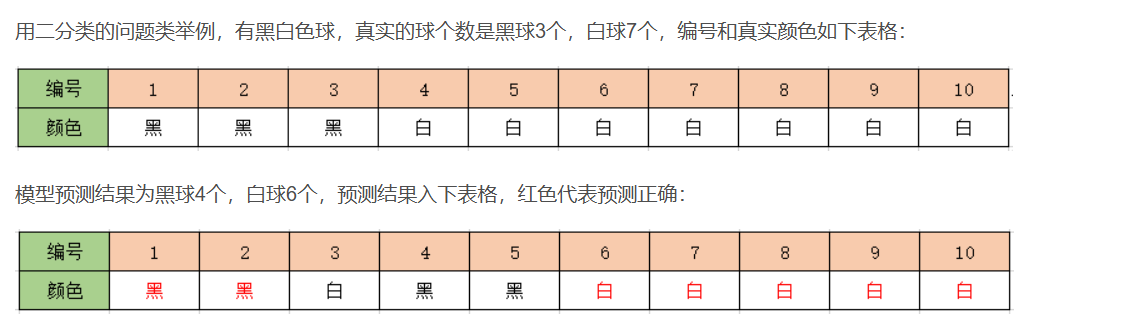
如果我们以黑球为正例标准，则可以统计出：

TP：2个，预测是黑色的，实际就是黑色的，即黑字红色部分。

FP：2个，预测是黑色的，实际是白色的，即黑字黑色部分，即编号4和5。

FN：1个，预测是白色的，实际是黑色的，即白字黑色部分，即编号3。

TN：5个。预测是白色的，实际是白色的，即白字红色部分。

Python实际使用

sklearn 的评估函数

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score

y_true = [1, 1, 1, 0, 0, 0, 0, 0, 0, 0]
y_pred = [1, 1, 0, 1, 1, 0, 0, 0, 0, 0]
print("acc:", accuracy_score(y_true, y_pred))
print("p:", precision_score(y_true, y_pred))
print("r:", recall_score(y_true, y_pred))
print("f1:", f1_score(y_true, y_pred))

输出结果为：

acc: 0.7 p: 0.5 r: 0.6666666666666666 f1: 0.5714285714285715

pyspark 的评估函数

from pyspark.mllib.evaluation import MulticlassMetrics
from pyspark import SparkConf, SparkContext

conf = SparkConf() \
    .setMaster("local") \
    .setAppName("Metrics-test")
sc = SparkContext(conf=conf)

predictionAndLabels = sc.parallelize([  #(预测值，真实值)
    (1.0, 1.0),
    (1.0, 1.0),
    (0.0, 1.0),
    (1.0, 0.0),
    (1.0, 0.0),
    (0.0, 0.0),
    (0.0, 0.0),
    (0.0, 0.0),
    (0.0, 0.0),
    (0.0, 0.0)])

metrics = MulticlassMetrics(predictionAndLabels)

print("acc:", metrics.accuracy)
print("p:", metrics.precision(1.0)) # 必须传入label值，否则统计的是类别0和类别1的均值
print("r:", metrics.recall(1.0))
print("f1", metrics.fMeasure(1.0))

tensorflow 的评估函数

import tensorflow as tf
train_graph = tf.Graph()
with train_graph.as_default():
    labels = tf.constant([1, 1, 1, 0, 0, 0, 0, 0, 0, 0])
    predicts = tf.constant([1, 1, 0, 1, 1, 0, 0, 0, 0, 0])
    
    # 返回的是一个二元组tuple
	accuracy = tf.metrics.accuracy(labels, predicts)
	precision = tf.metrics.precision(labels, predicts)
	recall = tf.metrics.recall(labels, predicts)
	f1 = tf.metrics.mean((2 * precision[1] * recall[1]) / (precision[1] + recall[1]), name='f1_score')
    
with tf.Session(graph=train_graph) as sess:
    sess.run(tf.local_variables_initializer())
    result = sess.run([accuracy, precision, recall, f1])
    print(result)

输出为：

[(0.0, 0.7), (1.0, 0.5), (1.0, 0.6666667), (0.0, 0.57142854)]

后面一个才是真实值

混淆矩阵 Confusion Matrix

针对两种测出同一种类型组的实验方式或对象测试的统计数据评估矩阵，常用于比较两种对象或方式的优劣程度或表诉某种实验方式预测结果的统计指标

一个经典的表示预测方式统计指标的混淆矩阵Confusion Matrix如下：

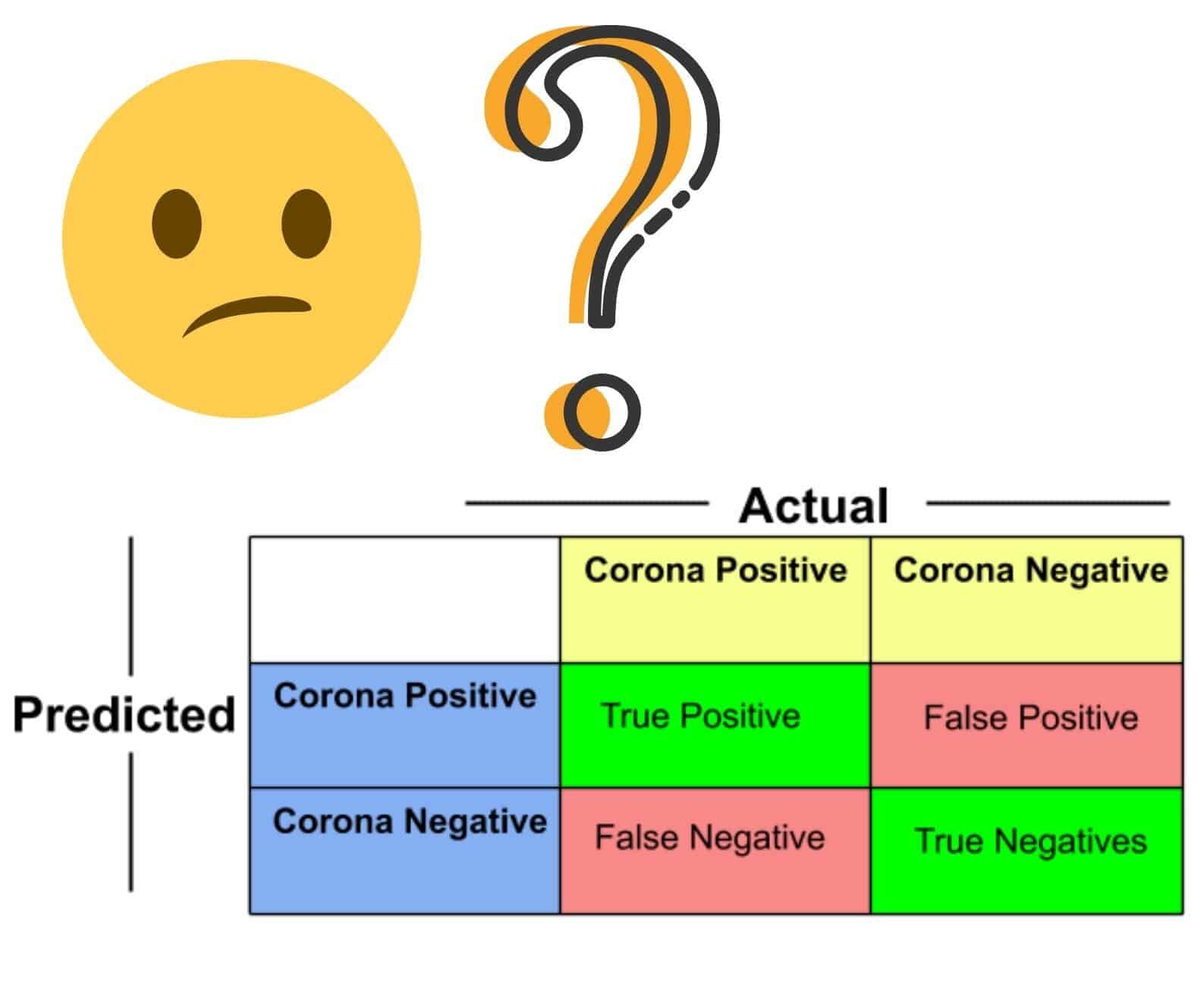
值得注意的是，在很多实验当中Actual并非实际客观的结论而是指定的一种F1较高的实验结果。

参考资料

准确度(accuracy)、精确率（precision)、召回率（recall）、F1值谈谈我的看法_recall f1-CSDN博客