MindSpore专题——第六章——函数式微分

发表于 2024-08-14 更新于 2024-08-16 分类于专题，机器学习， Mindspore ，基本概念阅读次数： Waline：本文字数： 8.4k 阅读时长 ≈ 30 分钟

函数式自动微分

神经网络的训练主要使用反向传播算法，模型预测值（logits）与正确标签（label）送入损失函数（loss function）获得loss，然后进行反向传播计算，求得梯度（gradients），最终更新至模型参数（parameters）。自动微分能够计算可导函数在某点处的导数值，是反向传播算法的一般化。自动微分主要解决的问题是将一个复杂的数学运算分解为一系列简单的基本运算，该功能对用户屏蔽了大量的求导细节和过程，大大降低了框架的使用门槛。

MindSpore使用函数式自动微分的设计理念，提供更接近于数学语义的自动微分接口grad和value_and_grad。下面我们使用一个简单的单层线性变换模型进行介绍。

这里总算是提到了反向传播，最近我看到了一系列视频有关Machine Learning，传送门如下：

🔴 World of Warships / USS Des Moines cut (youtube.com)

如果你试图看下去的话，可能会发现，事情好像突然变难了，似乎一群从未见过的知识组合在了一起，神经网络就像一个黑箱连着另一个黑箱，而你根本不知道如何优化它，使得黑箱在给定的输入下输出正确答案

神经网络到底代表了什么

首先让我们定义什么是神经：他是一个携带一个浮点数的结构，然后让我们看向神经网络

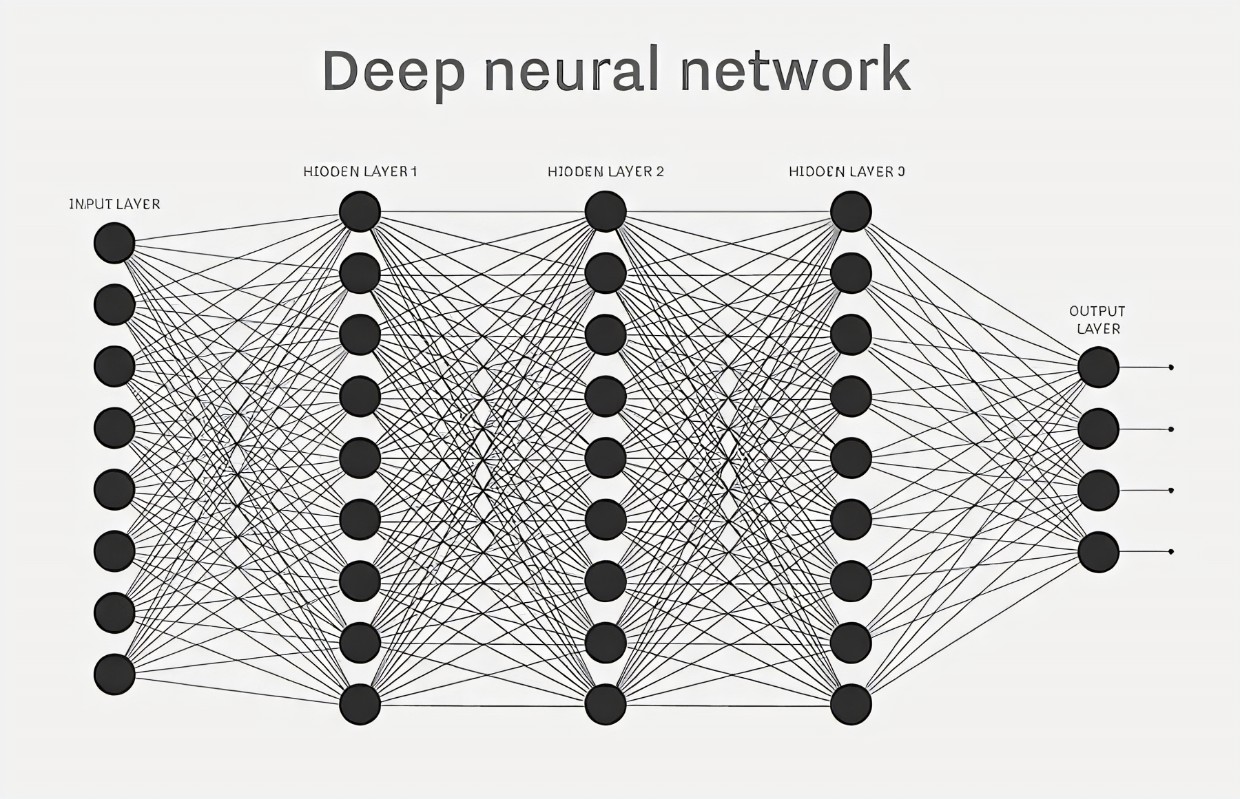
对于每一个点，我们从最后看起，显然，他们代表0-9，更准确的说，他们代表0-9的图像。为什么这样的网络是生效的呢？

因为分形思想，我们将一段连续的图像区分为一段一段，比如9是⚪在上而线条在下。4由多端线段1组成。而⚪和线条又可以继续再分，我们可以将神经网络中的每一个节点代表的数据想象成这种规律图案的集合。他们之间的传递就是图案在网络中不断组合。这也是为什么在网络中使用全连接的原因，因为每一个图案都能与其他任何图案组合。最终我们使图案变成了不断分形像素的组合。

但如何做到这一点呢？考虑我们前面提到的参数，权值。

这张图相信有很多人见过类似的图，实际上权值代表的就是神经网络之间的连线，假设我们让正权值在下表中为绿负权值在下表中为红，我们将这样描述一条“线段”：一段由红色包围的长条状绿色区域这样我们就能得出，如果这段线条是成立得话，比如确实原图这里存在一条线段，我们得到的这个神经节点上得值就会很接近1，否则就会很接近零。这就是权值得意义。但同时，我们会注意到神经得值是许多这样计算的累和，因此我们需要一个bias，偏差值将其计算到到0-1。

注意这里得权值和偏差值均是变量，是训练出来的。并且注意，我们并不知道机器是如何分形得，这取决于学习数据和使用的算法，以上只为举例理解。

如果将最初得神经网络拿去使用，你只会得到一大堆垃圾数据。我们都知道神经网络存在“进化”过程，但他是如何知道自己错得有多离谱的呢？

Cost Function（Maybe also loss function?）

初略的定义是他是输出的张量与正确的张量的差值平方和，比如，机器输出了一个全是0.5的10个数的张量，而正确答案是其中之一，那么 \[ \text{Cost} = (1-0.5) + 0.5*9 \] 显然这个数字更接近0，说明结果更加准确

考虑如何让模型表现得更好，显然是需要找到一组参数，使得每次输出的cost值最小。我们可以考虑这样一种方式，以参数作为输入，cost的值作为输出，而训练数据则是参数。

梯度下降 (Gradient Descent)

似乎难以理解，假设我们只有一个参数cost=f(c)，c是唯一的参数。于是变为了函数的最值问题，只需要求导数然后慢慢移动我们的初始点。很显然，一个函数在常数域上可能存在多个极大值而只有一个最大值。当我们从一个点出发寻找最大值时，很有可能（概率学上讲应该是绝对）我们只会找到一个极大值。即在神经网络中，我们不能保证我们的参数是最优的，只能保证我们的参数是局部最优的（这取决于我们的起始点）。

变到多维，我们意识到，一个数的导数是否只有正或负两种信息有效（代表是应该增加这个数还是减少这个数）。假定两个变量在一个点上的导数其中一个是另一个的三倍，这至少说明在该点的邻域内，这一变量应该减少的更多是正确的。（可能有一些函数存在极端的尖点导致错误，但这在神经网络中是低概率的，掌控好更改数据的大小即可）。

一个简单的例子是，维护好一个\[\nabla C\]矩阵，一阶导数对应的值高则其增加，反之则减少。

反向传播

从特殊到一般，我们先观察这样一个样例

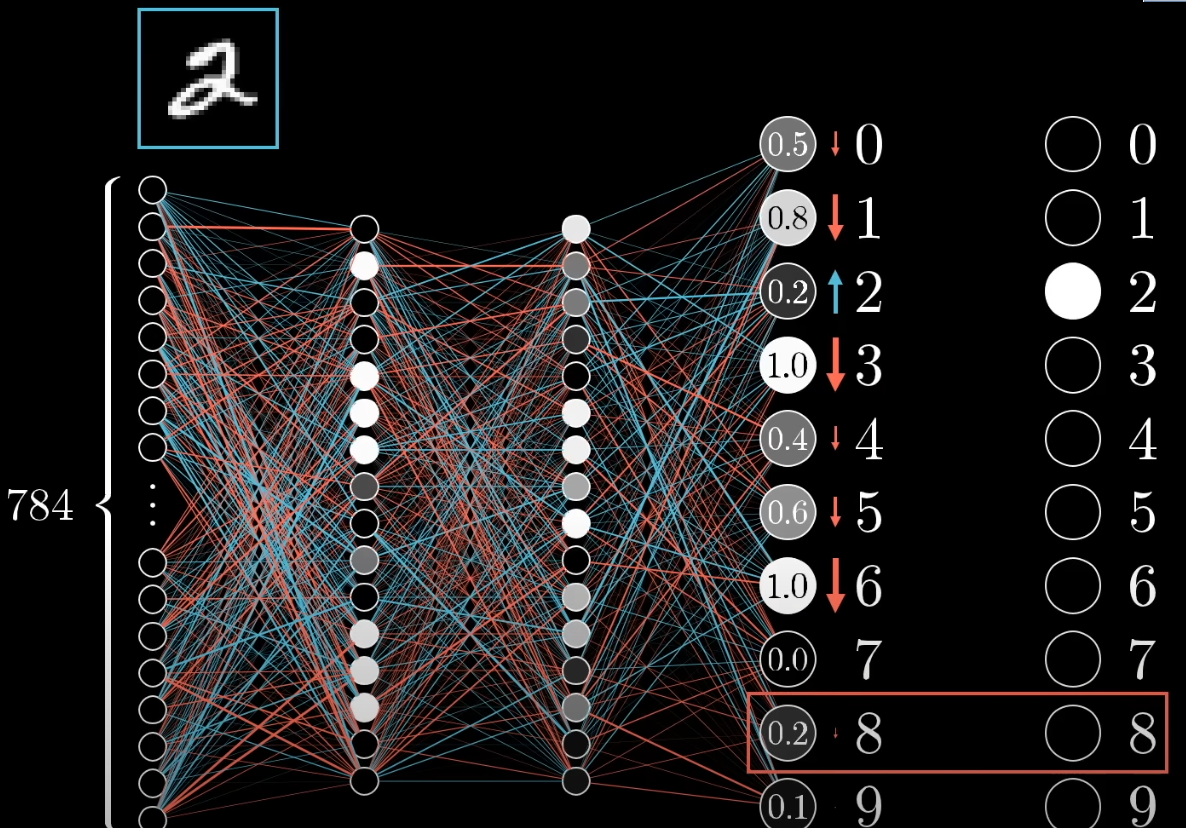
显然我们需要增加2，并且如果给我们要做的事情做出一个排序，增加2显然排在减少8之前。

因此，让我们继续看增加2所涉及的值

更改偏差值
更改权值（根据节点值）
更改上一层节点的值（根据权值）

我们对权值和边权同时改变，并统计下一层节点需要的变化对上一层的节点影响的累和

通过多组数据得出权值的总共改变值改变值。这就是随机梯度下降（Stochastic gradient descent）

下面简单讲一讲其他的名词解释

Mini-batches

和他的名字一样，这个技术就是将训练数据分为几组以提高收敛参数的效率

Backpropagation

反向传播是一种梯度下降法的应用，通过链式法则计算损失函数相对于每个权重的梯度，然后利用这些梯度来更新权重。

函数与计算图

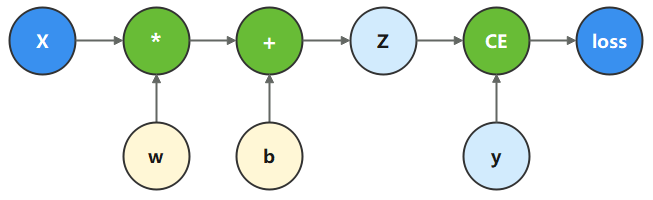
计算图是用图论语言表示数学函数的一种方式，也是深度学习框架表达神经网络模型的统一方法。我们将根据下面的计算图构造计算函数和神经网络。

在这个模型中，𝑥为输入，𝑦为正确值，𝑤和𝑏是我们需要优化的参数。

𝑥为输入
𝑦为正确值
𝑤和𝑏是我们需要优化的参数

即对应了原始数据，输出结果，权重和偏差

x = ops.ones(5, mindspore.float32)  # input tensor
y = ops.zeros(3, mindspore.float32)  # expected output
w = Parameter(Tensor(np.random.randn(5, 3), mindspore.float32), name='w') # weight
b = Parameter(Tensor(np.random.randn(3,), mindspore.float32), name='b') # bias

我们根据计算图描述的计算过程，构造计算函数。其中，binary_cross_entropy_with_logits 是一个损失函数，计算预测值和目标值之间的二值交叉熵损失。

解释一下Parameter(): Parameter 是 Tensor 的子类，当它们被绑定为Cell的属性时，会自动添加到其参数列表中，并且可以通过Cell的某些方法获取，例如 cell.get_parameters() 。

def function(x, y, w, b):
    z = ops.matmul(x, w) + b
    loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
    return loss

loss = function(x, y, w, b)
print(loss)

这里有复杂概念二值交叉熵损失，如果你不想深究只需要这是一个对参数的函数，当这个函数值最低时，整体参数就是一个准确率较高的局部最优解即可。

微分函数与梯度计算

为了优化模型参数，需要求参数对loss的导数：\[\frac{𝜕loss}{𝜕𝑤}\]和\[\frac{𝜕loss}{𝜕𝑏}\]，此时我们调用mindspore.grad函数，来获得function的微分函数。

这里使用了grad函数的两个入参，分别为：

fn：待求导的函数。

grad_position：指定求导输入位置的索引。

由于我们对\[𝑤\]和\[𝑏\]求导，因此配置其在function入参对应的位置(2, 3)。

使用grad获得微分函数是一种函数变换，即输入为函数，输出也为函数。

grad_fn = mindspore.grad(function, (2, 3))

grads = grad_fn(x, y, w, b)
print(grads)

(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 8.17961693e-02,  1.48393542e-01,  6.00685179e-03],
 [ 8.17961693e-02,  1.48393542e-01,  6.00685179e-03],
 [ 8.17961693e-02,  1.48393542e-01,  6.00685179e-03],
 [ 8.17961693e-02,  1.48393542e-01,  6.00685179e-03],
 [ 8.17961693e-02,  1.48393542e-01,  6.00685179e-03]]), Tensor(shape=[3], dtype=Float32, value= [ 8.17961693e-02,  1.48393542e-01,  6.00685179e-03]))

执行微分函数，即可获得\[𝑤\]、\[𝑏\]对应的梯度。可以注意到w,b的梯度与最初始的梯度是一致的。

Stop Gradient

通常情况下，求导时会求loss对参数的导数，因此函数的输出只有loss一项。当我们希望函数输出多项时，微分函数会求所有输出项对参数的导数。此时如果想实现对某个输出项的梯度截断，或消除某个Tensor对梯度的影响，需要用到Stop Gradient操作。

这里我们将function改为同时输出loss和z的function_with_logits，获得微分函数并执行。

def function_with_logits(x, y, w, b):
    z = ops.matmul(x, w) + b
    loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
    return loss, z

grad_fn = mindspore.grad(function_with_logits, (2, 3))
grads = grad_fn(x, y, w, b)
print(grads)

def function_stop_gradient(x, y, w, b):
    z = ops.matmul(x, w) + b
    loss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))
    return loss, ops.stop_gradient(z)

grad_fn = mindspore.grad(function_stop_gradient, (2, 3))
grads = grad_fn(x, y, w, b)
print(grads)

ops.stop_gradient(z):重点在该函数，表示屏蔽了z对梯度的影响，即仍只求参数对loss的导数。

这里解释一下一些api的含义

1	mindspore.grad(fn, grad_position=0, weights=None, has_aux=False, return_ids=False)

MindSpore

1	mindspore.numpy.matmul(x1, x2, dtype=None)

MindSpore

Auxiliary data

Auxiliary data意为辅助数据，是函数除第一个输出项外的其他输出。通常我们会将函数的loss设置为函数的第一个输出，其他的输出即为辅助数据。

grad和value_and_grad提供has_aux参数，当其设置为True时，可以自动实现前文手动添加stop_gradient的功能，满足返回辅助数据的同时不影响梯度计算的效果。

下面仍使用function_with_logits，配置has_aux=True，并执行。

1
2
3

grad_fn = mindspore.grad(function_with_logits, (2, 3), has_aux=True)
grads, (z,) = grad_fn(x, y, w, b)
print(grads, z)

神经网络梯度计算

前述章节主要根据计算图对应的函数介绍了MindSpore的函数式自动微分，但我们的神经网络构造是继承自面向对象编程范式的nn.Cell。接下来我们通过Cell构造同样的神经网络，利用函数式自动微分来实现反向传播。

首先我们继承nn.Cell构造单层线性变换神经网络。这里我们直接使用前文的𝑤、𝑏作为模型参数，使用mindspore.Parameter进行包装后，作为内部属性，并在construct内实现相同的Tensor操作。

这里出现了反向传播方法,并且是包装好的,建议读者仔细看一下代码并尝试自己运行一下。

# 定义神经网络模型
# Define model
class Network(nn.Cell):
    def __init__(self):
        super().__init__()
        self.w = w
        self.b = b

    def construct(self, x):
        z = ops.matmul(x, self.w) + self.b
        return z


# Instantiate model
model = Network()
# Instantiate loss function
loss_fn = nn.BCEWithLogitsLoss()


# Define forward function
def forward_fn(x, y):
    z = model(x)
    loss = loss_fn(z, y)
    return loss


# 注入损失函数
grad_fn = mindspore.value_and_grad(forward_fn, None, weights=model.trainable_params())
loss, grads = grad_fn(x, y)
print(grads)

总结输出（单次）

0.92031693
(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01]]), Tensor(shape=[3], dtype=Float32, value= [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01]))
计算多个参数的导数
(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 1.23408186e+00,  1.21728730e+00,  1.13000238e+00],
 [ 1.23408186e+00,  1.21728730e+00,  1.13000238e+00],
 [ 1.23408186e+00,  1.21728730e+00,  1.13000238e+00],
 [ 1.23408186e+00,  1.21728730e+00,  1.13000238e+00],
 [ 1.23408186e+00,  1.21728730e+00,  1.13000238e+00]]), Tensor(shape=[3], dtype=Float32, value= [ 1.23408186e+00,  1.21728730e+00,  1.13000238e+00]))
消除部分张量对梯度的影响
(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01]]), Tensor(shape=[3], dtype=Float32, value= [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01]))
Auxiliary data 辅助数据测试
(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01]]), Tensor(shape=[3], dtype=Float32, value= [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01])) [ 0.8580145   0.62723386 -0.44728255]      
开始实测网络模型的反向传播
(Tensor(shape=[5, 3], dtype=Float32, value=
[[ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01],
 [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01]]), Tensor(shape=[3], dtype=Float32, value= [ 2.34081909e-01,  2.17287347e-01,  1.30002365e-01]))

可见，除了在计算z的导数对梯度的影响情况下，均保持了相同的输出，并且可以观察到w,b的权值

二值交叉熵损失

以下的对数均为自然对数

Binary cross entropy 二元交叉熵是二分类问题中常用的一个Loss损失函数，在常见的机器学习模块中都有实现。就二元交叉熵这个损失函数的原理，简单地进行解释。下面是二元交叉熵损失函数的公式 \[ L=-\frac1N \sum_{i=1}^{N}[y_ilog(p_i)+(1-y_i)log(1-p_i)] \] 先不尝试理解他，先看看他是如何运作的

\[ L=\frac13[(1*log0.8+(1-1)*log(1-0.8))+(0*log0.2+(1-0)*log(1-0.2))+(0*log0.4+(1-0)*log(1-0.4))]=0.319 \\ \] 对于以上的案例计算损失函数，结果是0.31903

从熵来看交叉熵损失

信息量

信息量来衡量一个事件的不确定性，一个事件发生的概率越大，不确定性越小，则其携带的信息量就越小。

设\[X\]是一个离散型随机变量，其取值为集合\[X = {x_0,x_1,\dots,x_n}\]，则其概率分布函数为\[p(x) = Pr(X = x),x \in X\]，则定义事件\[X=x_0\]的信息量为： \[ I(x_0) = -\log(p(x_0)) \] 当\[p(x_0) = 1\]时，其携带的信息量为0。

熵

熵用来衡量一个系统的混乱程度，代表系统中信息量的总和；熵值越大，表明这个系统的不确定性就越大。具体而数学的讲，熵就是一个系统中所有信息量的期望。

信息量是衡量某个事件的不确定性，而熵是衡量一个系统（所有事件）的不确定性。

熵的计算公式 \[ H(x) = -\sum_{i=1}^np(x_i)\log(p(x_i)) \] 比较特殊的有二项分布熵 \[ \begin{eqnarray} H(X)&=&-\sum_{i=1}^n p(x_i)log(p(x_i))\\ &=&-p(x)log(p(x))-(1-p(x))log(1-p(x)) \end{eqnarray} \] 熵也有其他类型的计算公式，这里是信息学上的定义

其中\[p(x)\]为这件事发生的概率，\[-log(p(x_i))\]是事件\[x_i\]所携带的信息量。

可以看出，熵是信息量的期望值，是一个随机变量（一个系统，事件所有可能性）不确定性的度量。熵值越大，随机变量的取值就越难确定，系统也就越不稳定；熵值越小，随机变量的取值也就越容易确定，系统越稳定。

相对熵（Relative entropy）/ KL散度

wiki对相对熵的定义如下：In the context of machine learning, DKL(P‖Q) is often called the information gain achieved if P is used instead of Q.

即如果用P来描述目标问题，而不是用Q来描述目标问题，得到的信息增量。

在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

总结：相对熵也称为KL散度(Kullback-Leibler divergence)，表示同一个随机变量的两个不同分布间的距离。

设 \[p(x),𝑞(𝑥)\]分别是离散随机变量\[X\]的两个概率分布，则\[p\]对\[q\]的相对熵是： \[ D_{KL}(p \parallel q) = \sum_i p(x_i) log(\frac{p(x_i)}{q(x_i)}) \] 相对熵具有以下性质：

如果p(x)和q(x)的分布相同，则其相对熵等于0
\[D_{KL}(p∥q)≠D_{KL}(q∥p)𝐷_{𝐾𝐿}(𝑝∥𝑞)≠𝐷_{𝐾𝐿}(𝑞∥𝑝)\]，也就是相对熵不具有对称性。
\[D_{KL}(p∥q)≥0\]

总的来说，相对熵是用来衡量同一个随机变量的两个不同分布之间的距离。在实际应用中，假如p(x)是目标真实的分布，而q(x)是预测得来的分布，为了让这两个分布尽可能的相同的，就需要最小化KL散度。

交叉熵 Cross Entropy

设\[p(x),q(x)\]分别是离散随机变量\[X\]的两个概率分布，其中\[p(x)\]是目标分布，\[p\]和\[q\]的交叉熵可以看做是，使用分布\[q(x)\]表示目标分布\[p(x)\]的困难程度 \[ H(p,q) = \sum_ip(x_i)log\frac{1}{\log q(x_i)} = -\sum_ip(x_i)\log q(x_i) \] 将熵、相对熵以及交叉熵的公式放到一起， \[ \begin{align} H(p) &= -\sum_{i}p(x_i) \log p(x_i) \\ D_{KL}(p \parallel q) &= \sum_{i}p(x_i)\log \frac{p(x_i)}{q(x_i)} = \sum_i (p(x_i)\log p(x_i) - p(x_i) \log q(x_i)) \\ H(p,q) &= -\sum_ip(x_i)\log q(x_i) \end{align} \] 通过上面三个公式就可以得到 \[ D_{KL}(p,q) = H(p,q)- H(p) \] 其中，前一项\[H(p,q)\]就是\[p,q\]的交叉熵。在机器学习中，目标的分布\[p(x)\]通常是训练数据的分布是固定，即是\[H(p)\]是一个常量。这样两个分布的交叉熵\[H(p,q)\]也就等价于最小化这两个分布的相对熵\[D_{KL}(p \parallel q)\]

设\[p(x)\]是目标分布（训练数据的分布），我们的目标的就让训练得到的分布\[q(x)\]尽可能的接近\[p(x)\]，这时候就可以最小化\[D_{KL}(p∥q)\]，等价于最小化交叉熵\[H(p,q)\]。

为什么要用交叉熵做loss函数

在线性回归问题中，常常使用MSE（Mean Squared Error）作为loss函数，比如： \[ loss = \frac{1}{2m}\sum_{i=1}^m(y_i-\hat{y_i})^2 \] 这里的m表示m个样本的，loss为m个样本的loss均值。 MSE在线性回归问题中比较好用，那么在逻辑分类问题中还是如此么？

交叉熵在单分类问题中的使用

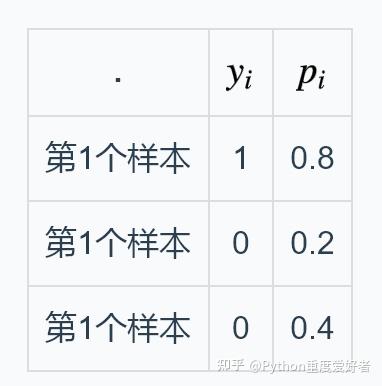
这里的单类别是指，每一张图像样本只能有一个类别，比如只能是狗或只能是猫。交叉熵在单分类问题上基本是标配的方法 \[ loss=-\sum_{i=1}^{n}y_ilog(\hat{y_i}) \] 上式为一张样本的loss计算方法。n代表着n种类别。举例说明,比如有如下样本

对应的标签和预测值

*	猫	青蛙	老鼠
Label	0	1	0
Pred	0.3	0.6	0.1

\[ \begin{eqnarray} loss&=&-(0\times log(0.3)+1\times log(0.6)+0\times log(0.1)\\ &=&-log(0.6) \end{eqnarray} \] 对应的一个batch的loss就是 \[ loss=-\frac{1}{m}\sum_{j=1}^m\sum_{i=1}^{n}y_{ji}log(\hat{y_{ji}}) \] m为当前batch的样本数

交叉熵在多分类问题中的使用

这里的多类别是指，每一张图像样本可以有多个类别，比如同时包含一只猫和一只狗和单分类问题的标签不同，多分类的标签是n-hot。比如下面这张样本图，即有青蛙，又有老鼠，所以是一个多分类问题

栗子

*	猫	青蛙	老鼠
Label	0	1	1
Pred	0.1	0.7	0.8

值得注意的是，这里的Pred不再是通过softmax计算的了，这里采用的是sigmoid。将每一个节点的输出归一化到[0,1]之间。所有Pred值的和也不再为1。换句话说，就是每一个Label都是独立分布的，相互之间没有影响。所以交叉熵在这里是单独对每一个节点进行计算，每一个节点只有两种可能值，所以是一个二项分布。前面说过对于二项分布这种特殊的分布，熵的计算可以进行简化。

同样的，交叉熵的计算也可以简化，即 \[ loss =-ylog(\hat{y})-(1-y)log(1-\hat{y}) \] 注意，上式只是针对一个节点的计算公式。这一点一定要和单分类loss区分开来。例子中可以计算为： \[ \begin{eqnarray} loss_猫 &=&-0\times log(0.1)-(1-0)log(1-0.1)=-log(0.9)\\ loss_蛙 &=&-1\times log(0.7)-(1-1)log(1-0.7)=-log(0.7)\\ loss_鼠 &=&-1\times log(0.8)-(1-1)log(1-0.8)=-log(0.8) \end{eqnarray} \] 单张样本的loss即为每一个batch的loss就是： \[ loss =\sum_{j=1}^{m}\sum_{i=1}^{n}-y_{ji}log(\hat{y_{ji}})-(1-y_{ji})log(1-\hat{y_{ji}}) \] 式中m为当前batch中的样本量，n为类别数。

从最大似然看交叉熵

设有一组训练样本$X= \{x_1,x_2,\cdots,x_m\}$ ,该样本的分布为$p(x)$ 。假设使用$\theta$ 参数化模型得到$q(x;\theta)$ ，现用这个模型来估计$X$ 的概率分布，得到似然函数 \[ L(\theta) = q(X; \theta) = \prod_i^mq(x_i;\theta) \] 最大似然估计就是求得$\theta$ 使得$L(\theta)$ 的值最大，也就是 \[ \theta_{ML} = arg \max_{\theta} \prod_i^mq(x_i;\theta) \] 对上式的两边同时取$\log$ ，等价优化$\log$ 的最大似然估计即log-likelyhood ，最大对数似然估计 \[ \theta_{ML} = arg \max_\theta \sum_i^m \log q(x_i;\theta) \] 对上式的右边进行缩放并不会改变$arg \max$ 的解，上式的右边除以样本的个数$m$ \[ \theta_{ML} = arg \max_\theta \frac{1}{m}\sum_i^m\log q(x_i;\theta) \]

和相对熵等价

上式的最大化$\theta_{ML}$ 是和没有训练样本没有关联的，就需要某种变换使其可以用训练的样本分布来表示，因为训练样本的分布可以看作是已知的，也是对最大化似然的一个约束条件。

注意上式的 \[ \frac{1}{m}\sum_i^m\log q(x_i;\theta) \] 相当于求随机变量$X$ 的函数$\log (X;\theta)$ 的均值 ，根据大数定理，随着样本容量的增加，样本的算术平均值将趋近于随机变量的期望。 也就是说 \[ \frac{1}{m}\sum_i^m \log q(x_i;\theta) \rightarrow E_{x\sim P}(\log q(x;\theta)) \] 其中$E_{X\sim P}$ 表示符合样本分布$P$ 的期望，这样就将最大似然估计使用真实样本的期望来表示 \[ \begin{aligned} \theta_{ML} &= arg \max_{\theta} E_{x\sim P}({\log q(x;\theta)}) \\ &= arg \min_{\theta} E_{x \sim P}(- \log q(x;\theta)) \end{aligned} \] 对右边取负号，将最大化变成最小化运算。

上述的推导过程，可以参考《Deep Learning》的第五章。但是，在书中变为期望的只有一句话，将式子的右边除以样本数量$m$ 进行缩放，从而可以将其变为$E_{x \sim p}\log q(x;\theta)$，没有细节过程，也可能是作者默认上面的变换对读者是一直。确实是理解不了，查了很多文章，都是对这个变换的细节含糊其辞。一个周，对这个点一直耿耿于怀，就看了些关于概率论的科普书籍，其中共有介绍大数定理的：当样本容量趋于无穷时，样本的均值趋于其期望。

针对上面公式，除以$m$后，$\frac{1}{m}\sum_i^m\log q(x_i;\theta)$ ，确实是关于随机变量函数$\log q(x)$ 的算术平均值，而$x$ 是训练样本其分布是已知的$p(x)$ ，这样就得到了$E_{x \sim p}(\log q(x))$ 。

\[ \begin{aligned} D_{KL}(p \parallel q) &= \sum_i p(x_i) log(\frac{p(x_i)}{q(x_i)})\\ &= E_{x\sim p}(\log \frac{p(x)}{q(x)}) \\ &= E_{x \sim p}(\log p(x) - \log q(x)) \\ &= E_{x \sim p}(\log p(x)) - E_{x \sim p} (\log q(x)) \end{aligned} \]

由于$E_{x \sim p} (\log p(x))$ 是训练样本的期望，是个固定的常数，在求最小值时可以忽略，所以最小化$D_{KL}(p \parallel q)$ 就变成了最小化$-E_{x\sim p}(\log q(x))$ ，这和最大似然估计是等价的。

和交叉熵等价

最大似然估计、相对熵、交叉熵的公式如下 \[ \begin{aligned}\theta_{ML} &= -arg \min_\theta E_{x\sim p}\log q(x;\theta) \\D_{KL} &= E_{x \sim p}\log p(x) - E_{x \sim p} \log q(x) \\H(p,q) &= -\sum_i^m p(x_i) \log q(x_i) = -E_{x \sim p} \log q(x)\end{aligned}\begin{aligned}\theta_{ML} &= arg \min_\theta E_{x\sim p}\log q(x;\theta) \\D_{KL} &= E_{x \sim p}\log p(x) - E_{x \sim p} \log q(x) \\H(p,q) &= -\sum_i^m p(x_i) \log q(x_i) = -E_{x \sim p} \log q(x)\end{aligned} \] 从上面可以看出，最小化交叉熵，也就是最小化$D_{KL}$ ，从而预测的分布$q(x)$ 和训练样本的真实分布$p(x)$ 最接近。而最小化$D_{KL}$ 和最大似然估计是等价的。

多分类交叉熵

多分类任务中输出的是目标属于每个类别的概率，所有类别概率的和为1，其中概率最大的类别就是目标所属的分类。 而softmax 函数能将一个向量的每个分量映射到$[0,1]$ 区间，并且对整个向量的输出做了归一化，保证所有分量输出的和为1，正好满足多分类任务的输出要求。所以，在多分类中，在最后就需要将提取的到特征经过softmax函数的，输出为每个类别的概率，然后再使用交叉熵 作为损失函数。

softmax函数定义如下： \[ S_i = \frac{e^{z_i}}{\sum^n_{i=1}e^{z_i}} \] 其中，输入的向量为$z_i(i = 1,2,\dots,n)$ 。

更直观的参见下图

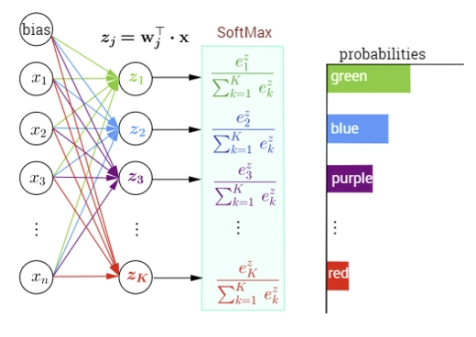
通过前面的特征提取到的特征向量为$(z_1,z_2,\dots,z_k)$ ，将向量输入到softmax函数中，即可得到目标属于每个类别的概率，概率最大的就是预测得到的目标的类别。

Cross Entropy Loss

使用softmax函数可以将特征向量映射为所属类别的概率，可以看作是预测类别的概率分布$q(c_i)$ ，有 \[ q(c_i) = \frac{e^{z_i}}{\sum^n_{i=1}e^{z_i}} \] 其中$c_i$ 为某个类别。

设训练数据中类别的概率分布为$p(c_i)$ ，那么目标分布$p(c_i)$ 和预测分布$q(c_i)$的交叉熵为

\[H(p,q) =-\sum_ip(c_i)\log q(c_i) \]

每个训练样本所属的类别是已知的，并且每个样本只会属于一个类别（概率为1），属于其他类别概率为0。具体的，可以假设有个三分类任务，三个类分别是：猫，猪，狗。现有一个训练样本类别为猫，则有：

\[\begin{align} p(cat) & = 1 \\ p(pig) &= 0 \\ p(dog) & = 0 \end{align} \]

通过预测得到的三个类别的概率分别为：$q(cat) = 0.6,q(pig) = 0.2,q(dog) = 0.2$ ，计算$p$ 和$q$ 的交叉熵为： \[ \begin{aligned} H(p,q) &= -(p(cat) \log q(cat) + p(pig) + \log q(pig) + \log q(dog)) \\ &= - (1 \cdot \log 0.6 + 0 \cdot \log 0.2 +0 \cdot \log 0.2) \\ &= - \log 0.6 \\ &= - \log q(cat) \end{aligned} \] 利用这种特性，可以将样本的类别进行重新编码，就可以简化交叉熵的计算，这种编码方式就是one-hot 编码。以上面例子为例， \[ \begin{aligned} \text{cat} &= (1 0 0) \\ \text{pig} &= (010) \\ \text{dog} &= (001) \end{aligned} \]

通过这种编码方式，在计算交叉熵时，只需要计算和训练样本对应类别预测概率的值，其他的项都是$0 \cdot \log q(c_i) = 0$ 。

具体的，交叉熵计算公式变成如下： \[ (p,q) = - \log q(c_i) \] 其中$c_i$ 为训练样本对应的类别，上式也被称为负对数似然（negative log-likelihood,nll）。

PyTorch中的Cross Entropy

PyTorch中实现交叉熵损失的有三个函数torch.nn.CrossEntropyLoss，torch.nn.LogSoftmax以及torch.nn.NLLLoss。

torch.nn.functional.log_softmax 比较简单，输入为$n$维向量，指定要计算的维度dim，输出为$log(Softmax(x))$。其计算公式如下：

\[ \text{LogSoftmax}(x_i) = \log (\frac{\exp(x_i)}{\sum_j \exp(x_j)}) \]

没有额外的处理，就是对输入的$n$维向量的每个元素进行上述运算。

torch.nn.functional.nll_loss 负对数似然损失（Negative Log Likelihood Loss)，用于多分类，其输入的通常是torch.nn.functional.log_softmax的输出值。其函数如下

1	torch.nn.functional.nll_loss(input, target, weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

input 也就是log_softmax的输出值，各个类别的对数概率。target 目标正确类别,weight 针对类别不平衡问题，可以为类别设置不同的权值；ignore_index 要忽略的类别，不参与loss的计算；比较重要的是reduction 的值，有三个取值：none 不做处理，输出的结果为向量；mean 将none结果求均值后输出；sum 将none 结果求和后输出。

torch.nn.CrossEntropyLoss就是上面两个函数的组合nll_loss(log_softmax(input))。

二分类交叉熵

多分类中使用softmax函数将最后的输出映射为每个类别的概率，而在二分类中则通常使用sigmoid 将输出映射为正样本的概率。这是因为二分类中，只有两个类别：{正样本，负样本}，只需要求得正样本的概率$q$,则$1-q$ 就是负样本的概率。这也是多分类和二分类不同的地方。

$\text{sigmoid}$ 函数的表达式如下： \[ \sigma(z) = \frac{1}{1 + e^{-z}} \] sigmoid的输入为$z$ ，其输出为$(0,1)$ ，可以表示分类为正样本的概率。

二分类的交叉熵可以看作是交叉熵损失的一个特列，交叉熵为 \[ \text{$Cross\_Entorpy$}(p,q) = -\sum_i^m p(x_i) \log q(x_i) \] 这里只有两个类别$x \in {x_1,x_2}$ ，则有 \[ \begin{aligned}\text{$Cross\_Entorpy$}(p,q) &= -(p(x_1) \log q(x_1) + p(x_2) \log q(x_2)) \end{aligned} \]

因为只有两个选择，则有$p(x_1) + p(x_2) = 1,q(x_1) + q(x_2) = 1$ 。设，训练样本中$x_1$的概率为$p$，则$x_2$为$1-p$; 预测的$x_1$的概率为$q$，则$x_2$的预测概率为$1 - q$ 。则上式可改写为 \[ \text{$Cross\_Entropy$}(p,q) = -(p \log q + (1-p) \log (1-q)) \] 也就是二分类交叉熵的损失函数。

总结

相对熵可以用来度量两个分布相似性，假设分布$p$是训练样本的分布，$q$是预测得到的分布。分类训练的过程实际上就是最小化$D_{KL}(p \parallel q)$，由于由于交叉熵 \[ H(p,q)= D_{KL}(p \parallel q) + H(p) \] 其中,$H(p)$是训练样本的熵，是一个已知的常量，这样最小化相对熵就等价于最小化交叉熵。

从最大似然估计转化为最小化负对数似然 \[ \theta_{ML} = -arg \min_\theta E_{x\sim p}\log q(x;\theta) \] 也等价于最小化相对熵。

回归问题

回归：人们在测量事物的时候因为客观条件所限，求得的都是测量值，而不是事物真实的值，为了能够得到真实值，无限次的进行测量，最后通过这些测量数据计算回归到真实值，这就是回归的由来。

回归分析的主要算法包括：

线性回归(Linear Regression)
逻辑回归（Logistic regressions）
多项式回归(Polynomial Regression)
逐步回归(Step Regression)
岭回归(Ridge Regression)
套索回归(Lasso Regression)
弹性网回归(ElasticNet)

最大似然估计

wiki定义：在统计学中，最大似然估计（英语：maximum likelihood estimation，简作MLE），也称极大似然估计，是用来估计一个概率模型的参数的一种方法。

原理

给定一个概率分布𝐷，已知其概率密度函数（连续分布）或概率质量函数（离散分布）为𝑓𝐷，以及一个分布参数𝜃，我们可以从这个分布中抽出一个具有𝑛个值的采样𝑋1,𝑋2,…,𝑋𝑛，利用𝑓𝐷计算出其似然函数：

若𝐷是离散分布，𝑓𝜃即是在参数为𝜃时观测到这一采样的概率；若其是连续分布，𝑓𝜃则为𝑋1,𝑋2,…,𝑋𝑛联合分布的概率密度函数在观测值处的取值。一旦我们获得𝑋1,𝑋2,…,𝑋𝑛，我们就能求得一个关于𝜃的估计。最大似然估计会寻找关于𝜃的最可能的值（即，在所有可能的𝜃取值中，寻找一个值使这个采样的“可能性”最大化）。从数学上来说，我们可以在𝜃的所有可能取值中寻找一个值使得似然函数取到最大值。这个使可能性最大的\[\hat 𝜃\]值即称为𝜃的最大似然估计。由定义，最大似然估计是样本的函数。

最大似然估计 - 维基百科，自由的百科全书 (wikipedia.org)