PGStudy-群体人工智能Part1-PSO
群体人工智能Part1-PSO
群体智能
群体智能(Swarm Intelligence, SI)已经引起了各个领域许多研究者的兴趣。Bonabeau将SI定义为“简单代理群体的突发集体智能”[1]。SI是自组织和分散系统的集体智能行为,例如,简单agent的人工群体。例如群居昆虫的群体觅食、合作运输、群居昆虫的筑巢、集体分类和聚类。自组织和劳动分工被认为是科学探究的必要属性。自组织被定义为系统在没有任何外部帮助的情况下将其代理或组件演化成适当形式的能力。Bonabeau et al.[1]也指出,自组织依赖于正反馈、负反馈、波动和多重交互的四个基本性质。正反馈和负反馈分别用于放大和稳定。同时,波动对随机性也很有用。当蚁群在其搜索区域内彼此共享信息时,就会发生多重交互。科学探究的第二个属性是劳动分工,它被定义为个体同时执行各种简单而可行的任务。这种分工使得蜂群能够解决复杂的问题,而这些问题需要个体协同工作。
目前较为常见(Well-Kown)的群体人工智能主要分为以下几个方面
遗传算法GA
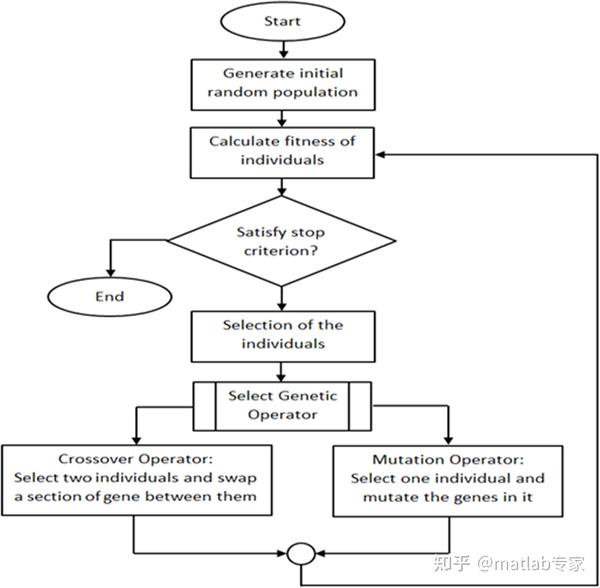
GA的操作开始于确定一个初始种群,无论是随机的还是使用一些启发式。适应度函数用来评估人口中的成员,然后根据表现对他们进行排名。一旦种群的所有成员已被评估,低秩染色体被省略和其余种群用于繁殖。
另一种可能的选择方案是使用伪随机选择,允许低秩染色体有机会被选择进行繁殖。交叉步骤随机选择剩余种群中的两个成员(最适染色体),并交换和交配它们。
遗传算法的最后一步是变异。在这一步中,突变算子在染色体的一个基因上随机突变。变异是遗传算法中至关重要的一步,因为它保证了问题空间的每个区域都能被到达。
蚁群优化ACO
见参考文献1
粒子群优化PSO
粒子群优化(PSO)是Kennedy和Eberhart在1995年[39]提出的一种优化技术。它使用一种简单的机制,模仿鸟类和鱼群的群体行为,引导粒子寻找全局最优解。Del Valle和他的合著者[40]用分离、对齐和内聚三种简单行为描述PSO,分别如图3所示。分离是避开拥挤的局部同伴的行为,对齐是向局部同伴的平均方向移动的行为。凝聚力是指向当地同伴的平均位置移动的行为。
PSO算法首先初始化种群。第二步是计算每个粒子的适应度值,更新个体和全局最佳值,更新粒子的速度和位置。重复第二步至第四步,直到满足终止条件[40,46 - 48]。在第一次迭代中,为了找到最佳的解决方案(探索),所有的粒子都分散开来。对每个粒子进行计算。根据邻域拓扑找到最优解,并更新群体中每个成员的个人和全局最优粒子。通过将所有粒子吸引到具有最佳解的粒子上来实现收敛。
差分进化(DE)算法
见参考文献1
人工蜂群算法ABC
见参考文献1
萤火虫群优化GSO
见参考文献1
布谷鸟搜索算法CSA
见参考文献1
群智PSO算法实现
1 | import numpy as np |
以上是一个简单的PSO算法以及其可视化实现,该算法实现了找道Rastrigin函数的最小值,该最小值(全局最优解)位于\((0,0)\),较常见的几个局部最优解分别位于\((\underline+0.5,\underline+0.5)\),以及\((\underline+20-30,\underline+20-30)\)之间
通过运行该文件应该可见
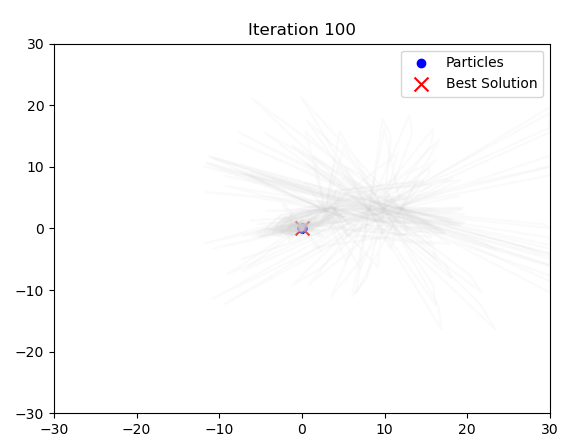
由1-100的粒子运动结果图,该结果图展现了30个粒子在100次的迭代过程中的表现,最终极大概率会定位到全局最优解\((0.0)\)附近
其中的核心代码如下所示
1 | for iteration in range(self.num_iterations): |
该段代码中的特定参数类似与机器学习过程中的超参例如inertia惯性参数,r1,r2等。
原版无可视化代码如下
1 | import numpy as np |
该段代码对目标函数略有更改,来自csdn博主闲人编程
参考文献
- Python实现群智能算法_群体智能算法python代码-CSDN博客
- 群体智能优化算法 - 知乎