abc353
abc353 (atcoder.jp)
C- Sigma Problem
第一个记录的abcC题
题意
对于正整数 \[x\] 和 \[y\] ,定义 \[f(x, y)\] 为 \[(x + y)$ 除以 \]10^8$ 的余数。
给你一个长度为 \(N\) 的正整数序列 \[A = (A_1, \ldots, A_N)\] 。求下面表达式的值:
\[\displaystyle \sum_{i=1}^{N-1}\sum_{j=i+1}^N f(A_i,A_j)\] . ### 题解
注意题目并非是完全模运算,注意到\(N\times N\times A_i\)刚刚好在longlong 边界上。并且\(A_i\times A_i\) 最多减少一次Mod,我们只需要找出mod1e8的次数即可。
刚刚开始我想的是二分,但实际上对于
1 | 1 50000000 5000000 9999999 9999999 999999 999999 999999 |
这样的数组是很难判断的,因为对于每一个数都只计算后面能跟他相加大于MOD的数(笔者写的时候突然注意到似乎如果更改为计算所有相加大于MOD的数,减去本身和本身再除以2就是正确的了),总之,这样的题解法很多。
我采用的是,双指针模拟一下,让这个相加大于模数的下标和本身下标取最大。
code
1 | void slove() { |
D - Another Sigma Problem
题意
对于正整数 \[x\] 和 \[y\] ,定义 \[f(x, y)\] 如下:
- 将 \[x\] 和 \(z\) 的十进制表示解释为字符串,并按此顺序连接,得到字符串 \[z\] 。将 \[f(x, y)\] 解释为十进制整数时,其值就是 \[z\] 的值。
例如, \[f(3, 14) = 314\] 和 \[f(100, 1) = 1001\] 。
给你一个长度为 \(N\) 的正整数序列 \[A = (A_1, \ldots, A_N)\] 。求下面表达式取模 \(998244353\) 的值:
\[\displaystyle \sum_{i=1}^{N-1}\sum_{j=i+1}^N f(A_i,A_j)\] .
题解
写了C顺便写D,这题反而比上一题简单,代数化一下函数,提一下公因子,计算一下公式就行,最后“前缀和”维护因子之一就行。
下面是代码code
1 | void slove() { |
E - Yet Another Sigma Problem
题意
对于字符串 \(x\) 和 \(y\) ,定义 \[f(x, y)\] 如下:
- \[f(x, y)\] 是 \[x\] 和 \[y\] 的最长公共前缀的长度。
给你一个由小写英文字母组成的 \(N\) 字符串 \[(S_1, \ldots, S_N)\] 。求以下表达式的值:
\[\displaystyle \sum_{i=1}^{N-1}\sum_{j=i+1}^N f(S_i,S_j)\] .
题解
还是注意到同样的\(O(N^2)\)是超出时间复杂度的,所以可以直接抛弃字符串hax计算两两前缀的做法。直接考虑整体。
很容易联想到字符树trie,因为在建立这个数据结构时就已经合并了前缀,我们维护一下每个节点的字符串数量即可。然后组合数计算一下答案
1 | int build(string& s){ |
F - Tile Distance
题意
问题陈述
瓷砖铺在一个坐标平面上。有两种瓦片:尺寸为 \[1\times1\] 的小瓦片和尺寸为 \[K\times K\] 的大瓦片,它们按以下规则摆放:
- 对于每一对整数 \((i,j)\) ,正方形
\[\lbrace(x,y)\mid i\leq x\leq i+1\wedge
j\leq y\leq j+1\rbrace\]
要么包含在一块小方砖中,要么包含在一块大方砖中。
- 如果 \[\left\lfloor\dfrac iK\right\rfloor+\left\lfloor\dfrac jK\right\rfloor\] 是偶数,则它包含在一个小方格中。
- 否则,它被包含在一个大瓦片中。
瓦片包括它们的边界,没有两个不同的瓦片有正的交集区域。
例如,当 \(K=3\) 时,瓦片的布局如下:
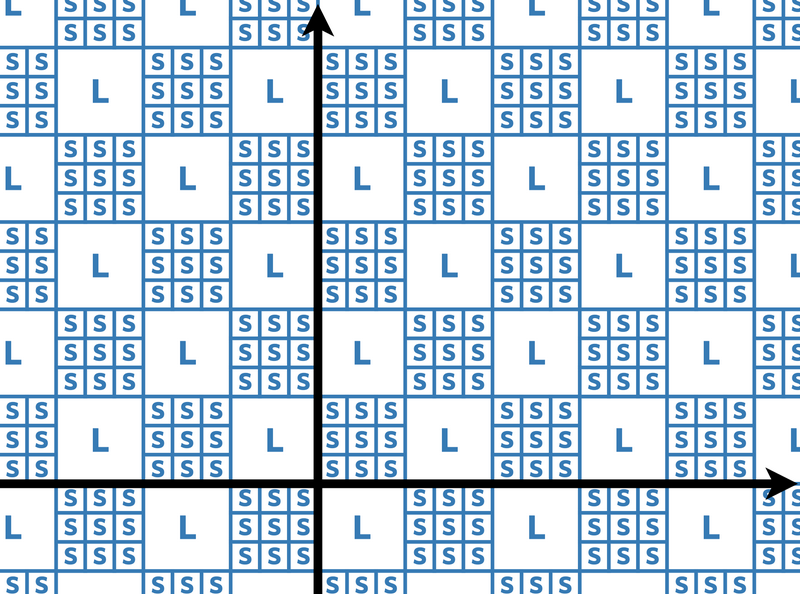
高桥开始于坐标平面上的点 \[(S_x+0.5,S_y+0.5)\] 。
他可以重复下面的动作任意多次:
- 选择一个方向(上、下、左或右)和一个正整数 \[n\] 。向该方向移动 \(n\) 个单位。
每次他从一张牌移动到另一张牌时,必须支付 \(1\) 的过路费。
求高桥到达点 \[(T_x+0.5,T_y+0.5)\] 所需的最小通行费。
题解
首先简化一下问题,就是求一个经过瓷砖数最少时的瓷砖数-1。
然后考虑哈密顿距离,可以发现,我们经过的瓷砖数显然是小于哈密顿距离的。然后针对题目数据较大,我们考虑一下走单纯走直线时的最短路。
可以发现,不断走最大瓷砖是最优的。
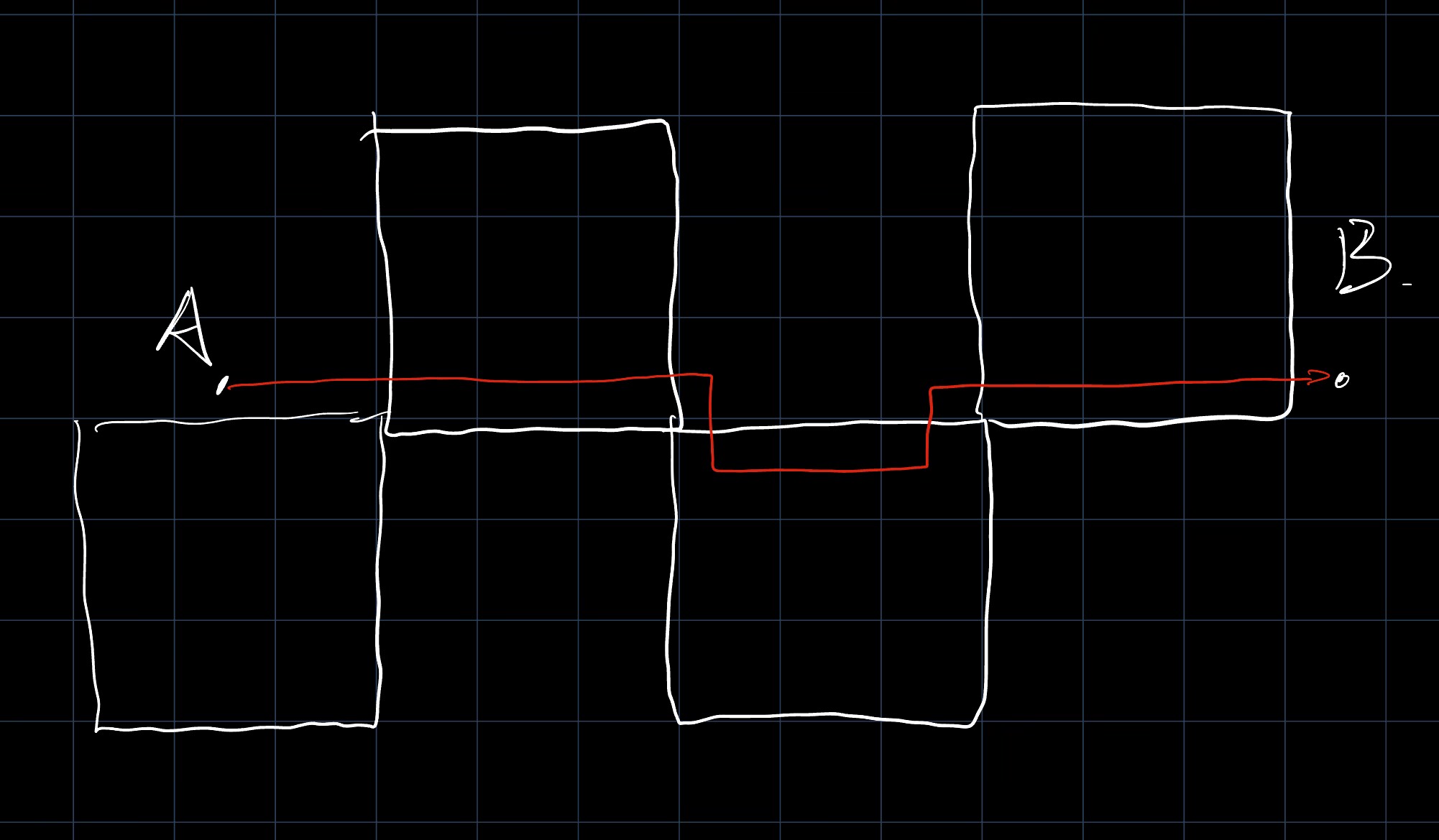
即上图所示的路径是最短的。
显然我们需要划分一下,定义一下中间这个走的最长的是从大瓷砖开始到最后一个大瓷砖结束,则经过的大瓷砖数为: \[ distance = \frac{d_s-d_a}{k} \times 2 -1 \] 其中定义\[d_s\]为走过直线长度,\[d_a\] 为两端长度,保证\[d_s - d_a \equiv k\]
可以看出,除去两边,实际上我们是在以k为方格边长的情况下对哈密顿距离乘了一个常数即\[\frac{2}{k}\],再减去\[1\]
但这样还是复杂了,以上只考虑了直线的情况,当我们涉及直线折角处会更为复杂,我们需要一个更简单解法。
根据上面的解释,我们发现在大瓷砖之间四向向转移所需要的成本为2,而当k==1时,我们的最短距离就等于哈密顿距离,当k>=2时,在小瓷砖之间的转移也是2,也就是说,除去极端情况,对小瓷砖到小瓷砖是不需要的(除非起点终点在小瓷砖)在大瓷砖之间转移总是更优的。
最后的结果形式上是切比雪夫距离
于是,计算从起点到大瓷砖终点到大瓷砖之间最多16种可能性的距离,取最小
1 | void slove() { |
G - Merchant Takahashi
题意
AtCoder 王国有 \(N\) 个城镇:城镇 \(1\) 、 \(2\) 、 \(\ldots\) 、 \(N\) 。从 \(i\) 镇到 \(j\) 镇,必须支付 \(C \times |i-j|\) 日元的过路费。
商人高桥正在考虑参加 \(M\) 个或更多即将到来的市场。
\(i\) /-市场 \[(1 \leq i \leq M)\] 由一对整数 \[(T_i, P_i)\] 描述,其中市场在城镇 \[T_i\] 举行,如果他参加将赚取 \[P_i\] 日元。
对于所有 \[1 \leq i < M\] , \[i\] 次市场在 \[(i+1)\] 次市场开始之前结束。他移动的时间可以忽略不计。
他从 \[10^{10^{100}}\] 日元开始,最初在 \[1\] 镇。通过优化选择参与哪些市场以及如何移动,确定他可以获得的最大利润-。
形式上,如果他在 \[M\] 个市场后获得最大资金额,那么 \[10^{10^{100}} + X\] 就是他的最终资金额。求 \[X\] 。
题解
显然的dp问题,如果你看不出来这是个dp问题建议你看一看再看最著名的 NP 问题之 TSP 旅行商问题 - 知乎 (zhihu.com),这篇blog,其中详细阐述了什么是np问题,几乎所有的np问题都是dp解的(因为他们找到多项式解是极其困难的)。记住这些问题,并在相似问题上找到他们的痕迹就是看是否为dp问题的关键。
详细到这一题,很简单的状态表示为 \[ f_i:到i城的最大profit \] 状态转移为: \[ f_i=max_{j=1}^n \left\{f_j-|i-j|\times C +p\right\} \] 对绝对值正负进行分类 \[ f_i=max_{j=1}^i \left\{f_j-i\times C+j\times C +p\right\}\\ f_i=max_{j=i}^n \left\{f_j-j\times C+i\times C +p\right\} \] 提出取最大中的常数项: \[ f_i=max_{j=1}^i \left\{f_j+j\times C \right\}+p-i\times C\\ f_i=max_{j=i}^{n} \left\{f_j-j\times C \right\}+p+i\times C \] 接下来就很简单了,维护最大值即可(使用两个线段树),官方题解是没有使用动态转移数组的,实际上在下面的代码中很多数组都是不必要的,只是为了方便读者理解。
1 |
|