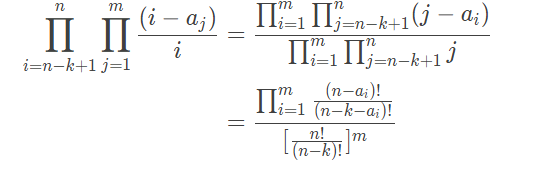luogu蓝桥5_19

B. 停车场

P10509 停车场 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题意

你有一片空地。这片空地可以视作一个一个 𝑛×𝑛 的正方形。空地外一圈为墙壁，你无法拆除它们。

现在你要在这片空地上规划停车位，使之成为一个停车场。你希望空地的左下角是停车场的出入口。出入口不能规划为停车位。空地和停车位都是 1×1的正方形，且正方形的每条边与墙壁平行或者垂直。

每个停车位都应该与至少一个空地四连通（即：停车场的上、下、左、右方至少有一个空地），且这个空地应当能通过若干次向上、下、左、右的移动，在不经过任何停车位的情况下到达出入口。

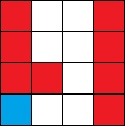
下图为 𝑛=4 时停车位数最多的放置方法之一，其中红色为车位，蓝色为出口，白色为空地。

img

请问 𝑛=2023 下最多能安排多少个停车位？

题解

这题真是一道神奇而又复杂的题目，我想如果国赛有这种题，可能刚开始心态就会爆炸

云剪贴板 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

洛谷官方对这题做出了非常详细的解释，但赛时证明是在过于繁琐，如果真的蓝桥，万一真有这种情况建议直接放掉这题。

这题的其中一种构造方法非常像“minecraft”里的鱼骨挖矿法即下图第二种

img

直接构造可得

答案为(2022+2021(6742-1)+67322+3)

D. 方差

P10511 方差 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题意

小 S 认为数学很简单，于是小 R 想要考考她。

小 R 给了小 S 一个序列 $a$，这个序列由 $m$ 段构成，第 $i$ 段被表示为 l r b，表示 $a_l,a_{l+1},\dots ,a_r$ 为 $b$，保证给出的任意两个区间不相交。

现在，小 R 有 $q$ 个问题。形如 l r，想让你查询区间 $[l,r]$ 的方差 $s^2$（需要注意：$l$ 可能等于 $r$，此时该段方差为 $0$）。

由于这个数字可能是个小数，小 R 不方便对答案，所以他想要小 S 求出 $(r-l+1{)}^2\cdot s^{2}mod998244353$。可以证明 $(r-l+1{)}^2\cdot s^2$ 一定是整数。

作为小 S 的好朋友，你能帮帮她吗？

题解

推导一下公式发现结果是

$$(r-l+1)\sum _{i=l}^{r-l+1}{a}_i^2-su{m}^2$$

预处理前缀和和前缀平方和，二分查找即可端点所在区间即可。

但一定需要注意多次取模，经过一个小时的鏖战，鉴定为取模题

void slove() {
	cin>>n>>m>>k;
	for(int i=1;i<=m;i++) {
		cin>>seg[i].l>>seg[i].r>>seg[i].v;
		seg[i].l %= MOD;
		seg[i].r %= MOD;
		seg[i].v %= MOD;
	}

	// sort(seg+1,seg+1+m);

	for(int i=1;i<=m;i++){
		segs[i] = segs[i-1] + ((((seg[i].r - seg[i].l  + 1) %MOD + MOD) %MOD) * seg[i].v) % MOD;
		segs[i] %= MOD;
		segs2[i] = segs2[i-1] + (((((seg[i].r - seg[i].l + 1) %MOD + MOD)%MOD) * seg[i].v %MOD)
				* seg[i].v) % MOD;
		segs2[i] %= MOD;
	}

	// for(int i=1;i<=m;i++) cout<<segs[i]<<' '<<segs2[i]<<endl;

	while(k--){
		int l,r;cin>>l>>r;
		int li = upper_bound(seg+1,seg+1+m,(Segment){l,0,0}) - seg - 1;
		int ri = upper_bound(seg+1,seg+1+m,(Segment){r,0,0}) - seg - 1;
		// cout<<"###"<<li<< ' ' << ri<<endl;

		if(li== ri)
    	{
      		cout<<0<<"\n";
      		continue;
    	}

		int msum = ((segs[ri-1] - segs[li])%MOD + MOD) % MOD;
		msum %= MOD;
		int rsum = (((r - seg[ri].l + 1) % MOD + MOD) % MOD * seg[ri].v) % MOD;
		rsum %= MOD;
		int lsum = ((seg[li].r - l + 1 + MOD) % MOD * seg[li].v) % MOD;
		lsum %= MOD;
		int msum2 = ((segs2[ri-1] - segs2[li])%MOD + MOD) %MOD;
		msum %=MOD;
		int rsum2 = ((((r - seg[ri].l + 1)%MOD + MOD) % MOD * seg[ri].v) % MOD
				* seg[ri].v) % MOD;
		rsum2%=MOD;
		int lsum2 = ((((seg[li].r - l + 1) %MOD + MOD) % MOD * seg[li].v) % MOD
				*seg[li].v) %MOD;
		lsum2 %=MOD;
		// cout<<"---"<<lsum << ' '<<msum<< ' '<<rsum<<endl;
		int sum = lsum + msum % MOD + rsum %MOD;
		sum %=MOD;
		int sum2 = lsum2 + msum2 % MOD + rsum2 %MOD;
		sum2%=MOD;
		// cout<<"####"<<sum<< ' '<< sum2<<endl;
		cout<<(((((r-l+1) %MOD + MOD) % MOD * sum2) % MOD -
							(sum*sum) %MOD) % MOD +MOD) %MOD<<endl;
	}
}

E. 序列合并

https://www.luogu.com.cn/problem/P10512?contestId=174155

题意

给定一个长度为 𝑛的非负整数序列 {$${𝑎}_{𝑛}$$}，你可以进行 𝑘次操作，每次操作你选择两个相邻的数，把它们合并成它们的按位或。

形式化地，一次操作中，你选择一个下标 𝑖i（1≤𝑖<𝑛1≤i<n），然后把原序列变成$$a_1,a_2,\cdots ,a_{i}or{a}_{i+1},a_{i+2},\cdots ,a_n$$。

求 𝑘次操作后所有数按位与的最大值。

题解

首先想到我们需要优先选高位。但此时注意到，对高位的选择也会影响到低位，我们必须考虑一个方式找到一个优的解使得答案最大

注意到合并的数本身代表了一个区间范围内的数，k次操作相当于选出了n-k个区间，如果要求答案为x则区间内的数并集为x，枚举每一个数显然是不现实的，但是我们可以通过二进制枚举来达到效果。

要记得从高到低枚举，因为每次记录t到ans中，我们实际限制了后面的取值。

我觉得比取模题简单

void slove() {
	cin>>n>>k;
	for(int i=1;i<=n;i++) cin>>a[i];

	int ans = 0;
	for(int i=29;~i;i--){
		int t = ans | (1<<i);

		int x = 0,cnt = 0;
		for(int i=1;i<=n;i++){
			x |= a[i];
			if((x & t) == t) cnt++,x=0;
		}
		if(cnt >= n - k) {
			ans = t;
			// cout<<cnt<<endl;
		}
	}

	cout<<ans<<endl;
}

F. 括号

https://www.luogu.com.cn/problem/P10513?contestId=174155

题意

圆给了你一个长度为 $n$ 的字符串 $S$，$S$ 仅由 ( 和 ) 构成。

她会对其做 $m$ 次操作，操作有两种类型：

1. 1 l r，她会翻转 $l$ 到 $r$ 的括号，即 ( 变 )，) 变 (。
2. 2 l r，她想知道区间 $[l,r]$ 中最长合法括号子序列的长度除以 $2$ 的答案。

圆认为以下的括号序列是合法的：

1. 空序列是一个合法序列。

2. 如果 A 是一个合法序列，则 (A) 也是一个合法序列。

3. 如果 A 和 B 都是合法序列，则 AB 也是一个合法序列。

圆认为，序列 $a$ 的子序列是满足 $1\le i_1<i_2<···<i_k\le n$ 的序列 $[a_{i_1},a_{i_2},...a_{i_k}]$。

由于操作太多了，她算不过来，请你帮帮她吧。

题解

洛谷真的要吓死我了，第六题线段树

对整个子串建立线段树，节点中维护当前区间左括号和右括号的的数量，合并左右节点即

$$ans=\mathrm{左}\mathrm{边}\mathrm{括}\mathrm{号}\mathrm{序}\mathrm{列}+\mathrm{右}\mathrm{边}\mathrm{括}\mathrm{号}\mathrm{序}\mathrm{列}+\mathrm{横}\mathrm{跨}\mathrm{中}\mathrm{间}\mathrm{的}\mathrm{括}\mathrm{号}\mathrm{序}\mathrm{列}$$

如何维护交换这一操作呢？

我们对每个节点维护两个不同的节点数据，一个是现在的，一个是假设翻转的。在交换时就交换这两个数据即可。（也可以都拆开成一个一个变量，也是可以的）。

struct node {
	int l,r,ans;
	node(int x=0,int y=0,int z=0){l=x,r=y,ans=z;}
};
struct tree{int tag;node t1,t2;}t[N<<2];
char s[N];

node merge(node x,node y)
{
    int cnt=min(x.l,y.r);
    return {x.l+y.l-cnt,x.r+y.r-cnt,x.ans+y.ans+cnt};
}
inline void pushup(int p){t[p].t1=merge(t[ls].t1,t[rs].t1);t[p].t2=merge(t[ls].t2,t[rs].t2);}
inline void pushson(int p){swap(t[p].t1,t[p].t2);t[p].tag^=1;}
inline void pushdown(int p){if(!t[p].tag) return;pushson(ls),pushson(rs);t[p].tag=0;}
inline void build(int p,int l,int r)
{
    if(l==r) return t[p].t2.r=t[p].t1.l=(s[l]=='('),t[p].t2.l=t[p].t1.r=(s[l]==')'),void();
    build(ls,l,mid);build(rs,mid+1,r);pushup(p);
}
inline void modify(int p,int l,int r,int s,int e)
{
    if(l>=s&&r<=e) return pushson(p);pushdown(p);
    if(mid>=s) modify(ls,l,mid,s,e);if(mid<e) modify(rs,mid+1,r,s,e);
    pushup(p);
}
inline node query(int p,int l,int r,int s,int e)
{
    if(l>=s&&r<=e) return t[p].t1;pushdown(p);
    if(e<=mid) return query(ls,l,mid,s,e);
    if(s>mid) return query(rs,mid+1,r,s,e);
    return merge(query(ls,l,mid,s,e),query(rs,mid+1,r,s,e));
}

void slove() {
	cin>>n;
	cin>>s+1;
	build(1,1,n);
	cin>>m;
	while(m--){
		int op,l,r;cin>>op>>l>>r;
		if(op == 1) {
			modify(1,1,n,l,r);
		}else {
			cout<<query(1,1,n,l,r).ans<<endl;
		}
	}
}

G.考试

https://www.luogu.com.cn/problem/P10514?contestId=174155

题意

有 $n$ 名同学去参加考试，考试有 $m$ 道题。

每个学生的实力是相同的，但是每道题的难度可能不同。第 $i$ 道题会有随机的 $a_i$ 名同学做错。

考试结束后，随机选出 $k$ 名同学，求出这些同学全部做对的概率。答案对 $998244353$ 取模。

题解

数学题。。。 懒得打公式了，如下

image-20240527221944431

预处理阶乘，快速幂分母时间复杂度为log(m)+n

处理分子时间复杂度为mlog(n)

ll qmi(ll a,ll b,ll mod = MOD){
	ll res = 1;
	for(;b;b>>=1){
		if(b&1) res = res * a % mod;
		a = a * a % mod;
	}
	return res;
}

void init(){
	fac[0] = infac[0] = 1;
	for(int i=1;i<N;i++){
		fac[i] = fac[i-1] *i % MOD;
		infac[i] = infac[i-1] * qmi(i,MOD-2,MOD) % MOD;
		// cout<<fac[i]<<' ' <<infac[i]<<endl;
	}
}

void slove() {
	cin>>n>>m>>k;

	int mx = 0;
	for(int i=1;i<=m;i++) cin>>a[i], mx= max(mx,a[i]);

	if(mx + k > n) {cout<<0<<endl;return ;}

	int inv = qmi(qmi(fac[n] % MOD * infac[n-k] %MOD, m, MOD),MOD-2,MOD);

	int factor = 1;
	for(int i=1;i<=m;i++){
		factor = factor * fac[n-a[i]] % MOD * infac[n-k-a[i]] % MOD;
	}

	cout<<factor*inv % MOD<<endl;
}

H. 转圈、按钮P4861

https://www.luogu.com.cn/problem/P10515?contestId=174155

题意

小 $\delta$ 喜欢转圈圈。

他有一个圈，被均匀分成了 $n$ 个格子，神奇的是，$n$ 是一个质数。第 $i$ 个格子上写着一个数 $i\times m$，他现在站在第一个格子上。

接下来他会看看脚下踩着的数是多少，然后向前走这么多格。他会一直反复这么做。

求最终被小 $\delta$ 踩到过的格子的数量。由于小 $\delta$ 有很多圈圈，所以他会问你很多次。

题解

这题和P4861撞了，所以我干脆贴这题了

根据欧拉定理$$a^{\varphi (p)}=1(modp)$$

因此$$\varphi (p)$$一定是答案的倍数，我们只需要枚举它的因子即可

ll qmi(ll a,ll b,ll mod = MOD){
	ll res = 1;
	for(;b;b>>=1){
		if(b&1) res = res * a % mod;
		a = a * a % mod;
	}
	return res;
}
int gcd(int x,int y){return y? gcd(y,x%y): x;}

void init(){}

int get_phi(int x){
	int res = x;
	if(!(x&1)) res >>= 1;

	for(int i=3;i*i<=x; i+= 2){
		if(x % i == 0){
			res -= res /i;
			while(x % i == 0) x/=i;
		}
	}
	if(x > 1) res -= res / x;

	return res;
}

void slove() {
	cin>>n>>m;
	if(gcd(n,m)!=1)puts("Let's go Blue Jays!");//无解
    else{
        int p=get_phi(n);//得到phi
        int mm=p;
        int tot = 0;
        for(int i=2;(i*i)<=mm;i++){
            if(mm%i)continue;
            pri[++tot]=i;
            while(mm%i==0){
                mm/=i;
                tim[tot]++;
            }
        }
        if(mm!=1){
            pri[++tot]=mm;
            tim[tot]=1;
        }

        int ss=1,qq=p;
        while(ss<=tot){
            for(int i=1;i<=tim[ss];i++){
                if(qmi(m,qq/pri[ss],n)==1)qq/=pri[ss];
                else break;
            }
            ss++;
        }
        cout<<qq<<endl;
    }
}